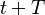Image stiching in OpenCV

Reference to http://ramsrigoutham.com/2012/11/22/panorama-image-stitching-in-opencv/

Main steps of the code:

1. Load two images;
2. Convert to gray scale;
3. Using SURF detector to find SURF descriptor in both images;
4. matching the SURF descriptor using FLANN Matcher;
5. Postprocessing matches to find good matches
6. Using RANSAC to estimate the Homography matrix using the matched SURF descriptors;
7. Warping the images based on the homography matrix

The image shows the definition of Homography which transforms 2d Planar point to the image plane. 

 The following image is shows the initial image and the matched SURF features of the two. Homography is derived from the left image to the right image.

Stiching image result.

Source Code

Resource to learn optimization

http://www.quora.com/Mathematical-Optimization/What-are-some-good-resources-to-learn-about-optimization#

Theory behind MPC

MPC is based on iterative, finite horizon optimization of a plant model. At time t the current plant state is sampled and a cost minimizing control strategy is computed (via a numerical minimization algorithm) for a relatively short time horizon in the future: . Specifically, an online or on-the-fly calculation is used to explore state trajectories that emanate from the current state and find (via the solution of Euler-Lagrange equations) a cost-minimizing control strategy until time . Only the first step of the control strategy is implemented, then the plant state is sampled again and the calculations are repeated starting from the current state, yielding a new control and new predicted state path. The prediction horizon keeps being shifted forward and for this reason MPC is also called receding horizon control.