6DOF equation (Euler Angles)
from http://www.mathworks.com/help/aeroblks/6dofeulerangles.html
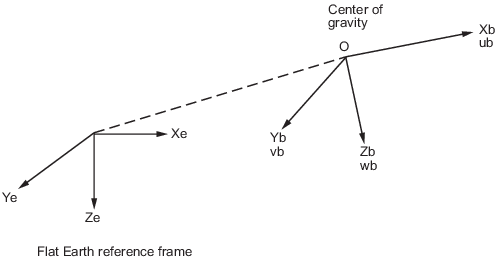
The 6DoF (Euler Angles) block considers the rotation of a body-fixed coordinate frame (Xb , Yb , Zb ) about a flat Earth reference frame (Xe , Ye , Ze ). The origin of the body-fixed coordinate frame is the center of gravity of the body, and the body is assumed to be rigid, an assumption that eliminates the need to consider the forces acting between individual elements of mass. The flat Earth reference frame is considered inertial, an excellent approximation that allows the forces due to the Earth's motion relative to the "fixed stars" to be neglected.
The translational motion of the body-fixed coordinate frame is given below, where the applied forces [Fx FyFz ]T are in the body-fixed frame, and the mass of the body m is assumed constant.

The rotational dynamics of the body-fixed frame are given below, where the applied moments are [L M N ]T, and the inertia tensor I is with respect to the origin O.

The relationship between the body-fixed angular velocity vector, [p q r]T, and the rate of change of the Euler angles,  , can be determined by resolving the Euler rates into the body-fixed coordinate frame
, can be determined by resolving the Euler rates into the body-fixed coordinate frame

Inverting J then gives the required relationship to determine the Euler rate vector.

背景知识
The cross product is anticommutative,
-
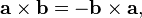
- The vector cross product also can be expressed as the product of a skew-symmetric matrix and a vector:[9]
-
where superscript T refers to the transpose operation, and [a]× is defined by:
![\mathbf{a} \times \mathbf{b} = [\mathbf{a}]_{\times} \mathbf{b} = \begin{bmatrix}\,0&\!-a_3&\,\,a_2\\ \,\,a_3&0&\!-a_1\\-a_2&\,\,a_1&\,0\end{bmatrix}\begin{bmatrix}b_1\\b_2\\b_3\end{bmatrix}](http://upload.wikimedia.org/math/b/b/0/bb0828317b64e54d924e3d9dabb54234.png)
![\mathbf{a} \times \mathbf{b} = [\mathbf{b}]_{\times}^\mathrm T \mathbf{a} = \begin{bmatrix}\,0&\,\,b_3&\!-b_2\\ -b_3&0&\,\,b_1\\\,\,b_2&\!-b_1&\,0\end{bmatrix}\begin{bmatrix}a_1\\a_2\\a_3\end{bmatrix}](http://upload.wikimedia.org/math/6/3/6/6366625aa8bc68fee9fc7c77659af07d.png)
![[\mathbf{a}]_{\times} \stackrel{\rm def}{=} \begin{bmatrix}\,\,0&\!-a_3&\,\,\,a_2\\\,\,\,a_3&0&\!-a_1\\\!-a_2&\,\,a_1&\,\,0\end{bmatrix}.](http://upload.wikimedia.org/math/3/8/e/38e1feb99d143b91383d2fb96ce8e10f.png)
No comments:
Post a Comment